Dragons

The dragon curve is my favorite fractal. One way to construct it is to fold a piece of paper in half many times and unfold. If all folds are right angles, you’ll get something that looks like…

If you had a piece of paper with width 0 that you could fold infinitely many times, it would look more like:

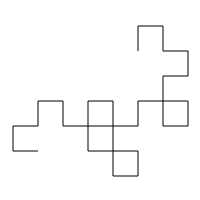
However, when you fold a piece of paper there are actually two directions you can make the fold. It turns out that not all fold patterns will generate a Heighway dragon, but they are all non-self intersecting. Here are some ‘degenerate’ dragons:

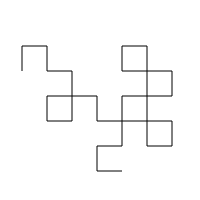
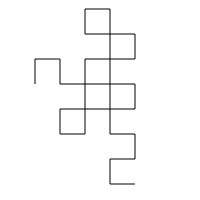
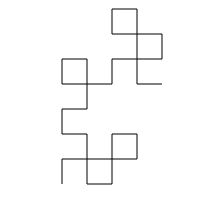
Not counting rotations and mirror images, for each number of folds n>1, there are 2^(n-2) unique dragons. I’m interested in other properties of dragons, and how they work when coded as binary strings. Some questions I have:

• Do all dragons tile the plane?
• Can you predict the dimensions of a dragon? What does it depend on?
• What would a “3d” dragon curve look like? What would be the algorithm to generate it?
• Could you generate a dragon curve (iterated function system that generates a non-self intersecting curve) on a base-3 alphabet? base-4? What would the algorithm be? How would you visualize it?
• How do binary operations like ~ (bitwise not) or +1 (add 1) effect the image?

I’m working on a few interactive demos using HTML5 to probe these questions. You can currently experiment with unfolding dragons from different signatures here.